Deriving the Geometric Formula for the Dot Product

In this article, we will learn the geometric interpretation of the dot product of two vectors.

Let me start by showing you the geometric formula to calculate the dot product of two vectors:

\(\alpha = \vec v \cdot \vec w = \|\vec v\| \|\vec w\| \cos \theta \)

So, the dot product of two vectors is:

The cosine of the angle between the two vectors scaled by (or multiplied by) the product of the lengths of the two vectors.

In the above equation we are multiplying the length of v times the length of w times the cosine of the angle between v and w vectors.

Angle Between Any Two Vectors

Now, first lets understand how to find or calculate the angle between two vectors.

\(\alpha = \|\vec v\| \|\vec w\| \cos \theta\)

This is our original equation. First, lets divide the length of v times the length of w.

\( \frac{\alpha}{\|\vec v\| \|\vec w\|} = \cos \theta\)

Now, we need to apply inverse of cosine to eliminate the cosine on the right hand side.

\( \arccos\!\left(\frac{\alpha}{\|\vec v\| \|\vec w\|}\right) = \theta\)

We denote the inverse of cosine as “arccos”.

So, now we got that the angle between any two vectors is the inverse cosine of the dot product of two vectors divided by the product of the lengths of the two vectors.

We derived this formula for the 2D case, but it will work for any n dimensional vectors.

Now, you might remember from your high school days, that:

The cosine of an angle can never be less than -1 and can never be greater than +1.

Now, this fact gives us some interesting insights:

• The dot product of two vectors can be negative only because of the cosine of the angle of two vectors (because the product of the length of the two vectors can be greater than or equal to 0 but can’t be negative as length can’t be negative)

• If the angle between the two vectors is less than 90 degree, then the cosine of that angle will be greater than 0, making the dot product of the two vectors greater than 0

• If the angle between the two vectors is greater than 90 degree, then the cosine of that angle will be smaller than 0, making the dot product of the two vectors smaller than 0

• If the angle between the two vectors is equal to 90 degree, then the cosine of that angle will be 0, making the dot product of the two vectors equal to 0. (This has a special name called “Orthogonal”.)

• If the angle between the two vectors is 0 degree (both the vectors are pointing in the same direction), then the cosine of that angle will be 1, making the dot product of the two vectors equal to whatever the product of the length of the two vectors will be.

Now, let me show you how the algebraic formula and the geometric formula are the same. Let’s see the proof:

We want to prove that:

\(\alpha =\mathbf{a}^\top\mathbf{b}=\sum_{i=1}^{n} a_i b_i = \cos \theta \|\vec a\| \|\vec b\|\)

We want to show that the algebraic definition (the sum of products of corresponding components) equals the geometric definition (the product of magnitudes times the cosine of the angle between them).

Law of Cosines

This proof relies on something called “The Law of Cosines”. First, let me proof this law of cosines to you.

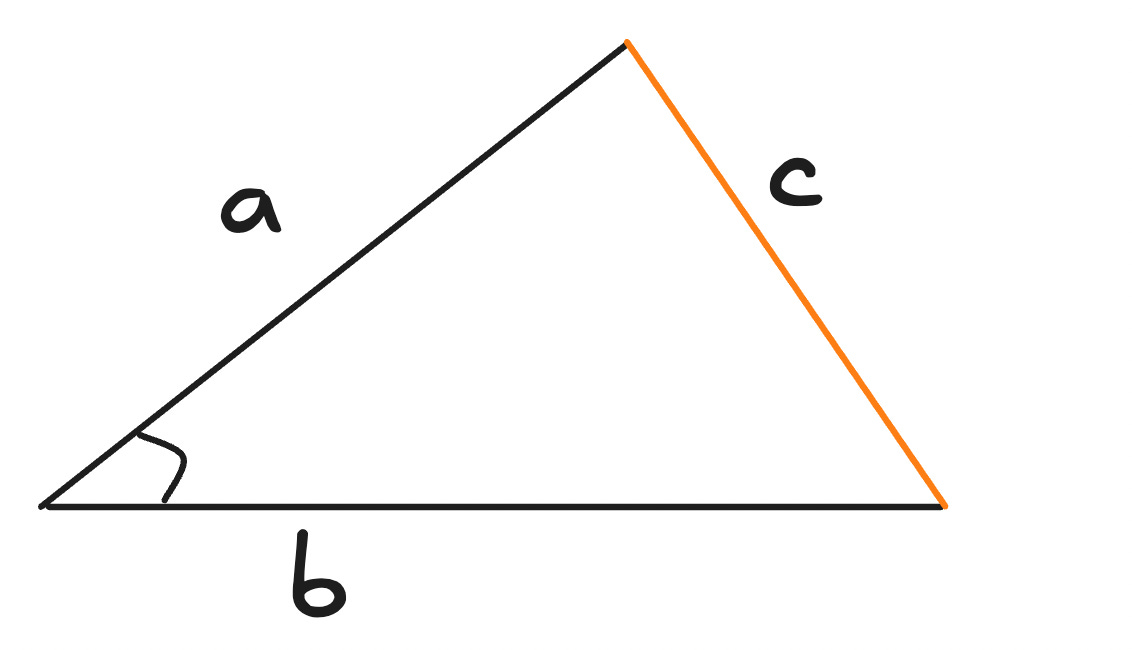
Let’s take the below triangle for this proof:

If this were a right triangle, we could have find the length of c using pythagorus theorem but when we don’t have a right triangle, we can use the law of cosines to get the length of c.

Let’s start the proof:

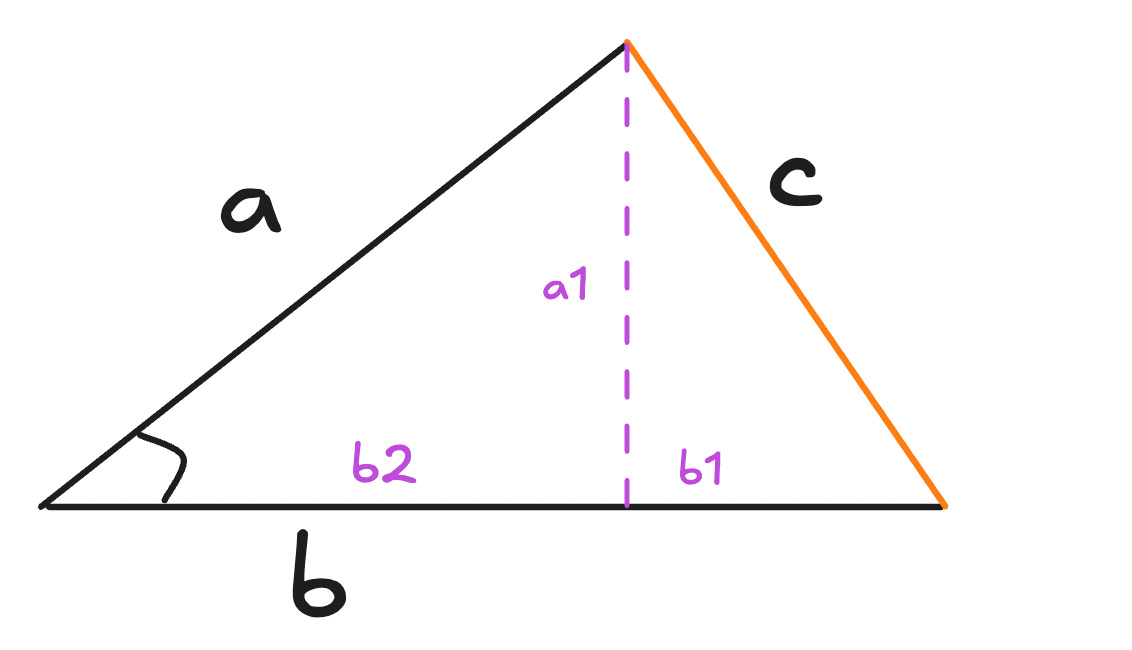
Let’s draw a perpendicular line from the intersecting point of a and c:

Now, you can see we have two right triangles.

So, now the length of b is length of b1 + length of b2:

\(b = b1 + b2\)

Now, our aim is to get a1 and b1. Once we get those values we can easily find the value of c. Let’s do that

First, lets find the value of b2:

So, the cosine of the angle is:

\(\cos \theta = \frac{b2}{a}\)

\( a \cos \theta = b2\)

Now we got b2, lets now get the value of a, so that we can easily get the value of a1:

\(\sin \theta = \frac{a1}{a} \)

\(a1 = a\sin \theta \)

Now, that we have a1, lets find out the value of b1 in terms of b2 and b:

\(b1 = b-b2 = b-a\cos \theta\)

Now, we have both a1 and b1. Finally we can start working on finding the length of c:

By using pythagorus theorem, we can say:

\( c^2 = a1^2 + b1^2\)

\(c^2 = a^2\sin^2\theta + (b-a\cos\theta)^2\)

\(c^2 = a^2\sin^2\theta + b^2 + a^2\cos^2\theta - 2ab\cos\theta \)

Now, lets take a^2 as common:

\(c^2 = a^2(\sin^2\theta+\cos^2\theta) + b^2 - 2ab\cos\theta\)

As we know sin square + cos square is equal to 1:

\(c^2 = a^2 + b^2 - 2ab\cos\theta \)

This final equation is the law of cosines

Now, we are in a position to define the value of c with known terms a and b.

If the theta = 0, then you can see we will get the pythagorus theorem. In fact, pythagorus theorem is really just a special case of law of cosines

Ok, now that we know about law of cosines, lets get back to our linear algebra concept and convert what we learned in terms of vectors:

\( \|\vec c\|^2 = \|\vec a\|^2 + \|\vec b\|^2 - 2\,\|\vec a\|\,\|\vec b\|\cos\theta \)

we can write this as:

\( \|\vec a - \vec b\|^2 = \|\vec a\|^2 + \|\vec b\|^2 - 2\,\|\vec a\|\,\|\vec b\|\cos\theta \)

We already know this from subtraction of vectors section.

Now, we can again write the above equation like this:

\( (\vec a - \vec b)^\top(\vec a - \vec b)=\|\vec a\|^2 + \|\vec b\|^2 - 2\,\|\vec a\|\,\|\vec b\|\cos\theta\)

we can rewrite this again as this:

\(\vec a^\top \vec a + \vec b^\top \vec b - 2\,\vec a^\top \vec b =\|\vec a\|^2 + \|\vec b\|^2 - 2\,\|\vec a\|\,\|\vec b\|\cos\theta\)

Now, you can see we know that:

\(\vec a^\top \vec a = \|\vec a\|^2 \\ \vec b^\top \vec b = \|\vec b\|^2\)

So, we can simplify the above equation as:

\(\vec a^\top \vec b = \|\vec a\|\,\|\vec b\|\cos\theta \)

Awesome, we started with a goal to prove that both the algebraic and geometric equation of the dot product of two vectors are the same and we did it. I know its a long one but we also understood a lot of things including the law of cosines.

I’ll see in the next one. Till then, Goodbye!