Geometric Understanding of Vector Addition and Subtraction
Now that you know what vectors are, its time to learn how to work with them. We will learn how to add and subtract vectors. We will learn this in both algebraic and geometric way.
Let’s start.
Source code for Python and Manim —> https://github.com/MrSheerluck/linear-algebra/tree/main/vectors/addition-subtraction
Vector Addition - Algebraic Way
The first thing you should remember is that whenever you are adding or subtracting 2 vectors, the dimensionality (the number of elements) of both the vectors should be same.
Algebraically, adding elements of vectors is really easy, you just need to add corresponding elements of the 2 vectors. It’s simple addition. Let me explain with some examples
For example:
Here, both the vectors have same dimensionality (total number of elements = 2 for each vector).
How to calculate the final value of the resultant vector:
First, add
1and3, that’ll give you4.Then, add
2and4, that’ll give you6.
Just simple arithmetic, nothing fancy.
Another example with 3 elements:
Vector Addition - Geometric Way
Geometrically, you put the tail of one vector at the head of another vector. Let me show you this visual example to make you understand it better.
In the above video, you can see we have:
First vector goes to (3,1), after that the second vector starts and moved 1 unit towards x and 3 units towards y. The final coordinate that we arrived is (4,4).
Vector Subtraction - Geometric Way
Geometrically, vector subtraction is completely similar to addition except one thing.
When you are subtracting two vectors, multiply the second vector with -1.
Yes, we can multiply scalar values with vectors, don’t worry I’ll explain about it in the next article. For now, just to understand vector subtraction, take my word for it and multiply
-1with the second vector.
For example:
Simple subtraction, but what I mean when I said “Vector subtraction = First Vector + (-1) * second vector”. Let me show you the above example using addition:
See, you got the same thing as your output.
Look at this video to understand the geometrical intuition:
First, the vector goes to (3, 1). Then the second vector is reversed, so it moves 1 unit left and 3 units down. After applying this reversed vector, the final coordinate we arrive at is (2, −2).
Now, lets understand how to do these operations in python.
Vector Addition in Python
I’m only showing addition as you just saw subtraction is really the same thing with -1 multiplied with the second vector.
First, lets import what we imported in last article:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# two vectors in R2
v1 = np.array([ 3, -1 ])
v2 = np.array([ 2, 4 ])
v3 = v1 + v2
# plot them
plt.plot([0, v1[0]],[0, v1[1]],'b',label='v1')
plt.plot([0, v2[0]]+v1[0],[0, v2[1]]+v1[1],'r',label='v2')
plt.plot([0, v3[0]],[0, v3[1]],'k',label='v1+v2')
plt.legend()
plt.axis('square')
plt.axis((-6, 6, -6, 6 ))
plt.grid()
plt.show()
Now, let me explain the code
Setting Up Our Vectors
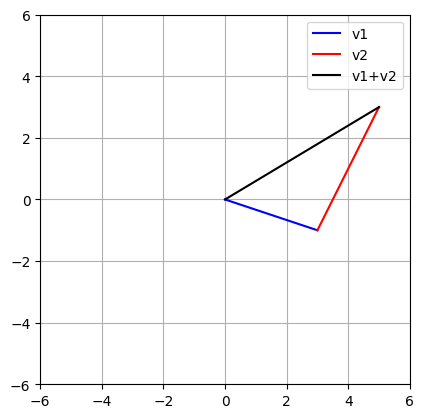
v1 = np.array([ 3, -1 ])
v2 = np.array([ 2, 4 ])
v3 = v1 + v2
We create two vectors and add them. NumPy handles the element-wise addition automatically: 3 + 2 = 5 and -1 + 4 = 3, so v3 becomes [5, 3].
Visualizing the Addition
plt.plot([0, v1[0]], [0, v1[1]], 'b', label='v1')
This draws v1 in blue from origin (0,0) to (3, -1).
plt.plot([0, v2[0]]+v1[0], [0, v2[1]]+v1[1], 'r', label='v2')
We draw v2 in red, but start it where v1 ended. The +v1[0] and +v1[1] shift the starting point (this is the “tail to head” approach from the video)
plt.plot([0, v3[0]], [0, v3[1]], 'k', label='v1+v2')
Finally, we draw the resultant vector in black directly from origin to (5, 3).
The remaining lines (plt.legend(), plt.axis(), etc.) just format the plot with labels, grid, and viewing window.
That’s it, now you know vector addition and subtraction both in algebraic and geometric way. I hope you had fun reading this quick article.
This is how I plan to keep all of my articles, so that you can quickly read and learn something in 5 minutes.
In the next article, we will cover vector scalar multiplication, till then happy learning. Good bye!


Already read this really indepth and simplified explaination of vector . you literally explain it clear. Previously these concepts feels like heAVY. Really liked the animated part.