Vector Cross Product Explained With Geometric Understanding

In this article, we are going to learn about another way to multiply two vectors using cross product. We will learn the algebraic formula to compute the cross product and then we will also see the geometric interpretation of the cross product.

Somethings you need to know before learning about vector cross product:

• Vector cross product is defined only for two 3D vectors, no less than 3 or no greater than 3 dimensions.

• The resultant vector will be of 3 dimensions too

Some other day, I’ll explain in detail and with visuals why we only have cross product for 3d vectors

Let’s start by looking at the formula, then we will understand why its this way and make sense of this:

\(\begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix} \times \begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix} \begin{bmatrix} a_2 b_3 - a_3 b_2 \\ a_3 b_1 - a_1 b_3 \\ a_1 b_2 - a_2 b_1 \end{bmatrix}\)

So, we have 2 3d vectors and you can see we are multiply elements in a cross like (a2 and b3, a3 and b2), (a3 and b1, a1 and b3), (a1 and b2, a2 and b1).

Now, lets see what the cross product means geometrically:

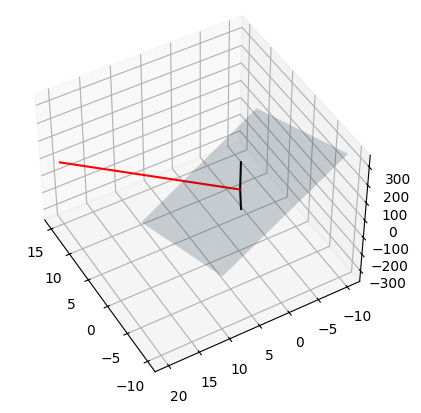
If you have 2 vectors in 3 dimensions, those two vectors can be used to define a plane. This is a concept in euclidean geometry that says any two distinct vectors can form a unique plane.

So, there is a unique plane that can be defined by these two vectors.

Now, when you compute the cross product, that gives you the third vector. This resultant vector will be orthogonal to the plane meaning it’ll be at a right angle to the entire plane.

Now, lets try to this cross product using python and then we will wrap up.

Cross Product in Python

Let’s start by importing the standard stuff

import numpy as np
import matplotlib.pyplot as plt

# create vectors
v1  = [ -3,  2, 5 ]
v2  = [  4, -3, 0 ]

# Python's cross-product function
v3a = np.cross( v1,v2 )

print(v3a)

fig = plt.figure()
# ax = fig.add_subplot(projection='3d')
ax = plt.axes(projection = '3d')

# draw plane defined by span of v1 and v2
xx, yy = np.meshgrid(np.linspace(-10,10,10),np.linspace(-10,10,10))
z1 = (-v3a[0]*xx - v3a[1]*yy)/v3a[2]
ax.plot_surface(xx,yy,z1,alpha=.2)

## plot the two vectors
ax.plot([0, v1[0]],[0, v1[1]],[0, v1[2]],'k')
ax.plot([0, v2[0]],[0, v2[1]],[0, v2[2]],'k')
ax.plot([0, v3a[0]],[0, v3a[1]],[0, v3a[2]],'r')

ax.view_init(azim=150,elev=45)
plt.show()

We take two vectors v1 and v2 and used numpy’s built-in cross function to calculate the cross product and then we are printing the vector. After that we all the code is about plotting that in 3d. I’m not explaining that as its a linear algebra series, I don’t want to explain all the matplotlib concepts. I hope you can understand.

I hope you understood cross product in an intuitive way. In the next one, we will learn about transpose. Till then Goodbye!